With the proliferation of devices running their own email programs, settings for POP3, SMTP, and now more frequently IMAP are a popular request for the various email services.
For a long time, Microsoft didn’t provide the ability to connect to a desktop email program, but they added it to Hotmail a few years ago. With the transition to Outlook.com as Hotmail’s replacement, that functionality remains.
Become a Patron of Ask Leo! and go ad-free!
Email programs
Various desktop and mobile email programs will ask for this information in a variety of ways and in different places.
Typically, when you set up an email program, you will configure one or more email accounts. An account includes:
- Your email address
- Your account user name (sometimes, this is the same as or derived from your email address)
- Your account password
 As you enter this information, your email program may also ask about the protocols that it will use to communicate to the servers of your email service provider.
As you enter this information, your email program may also ask about the protocols that it will use to communicate to the servers of your email service provider.
That’s what we’ll go over in Hotmail/Outlook.com with this article1.
SMTP
SMTP is used to send mail.
The SMTP configuration parameters for Outlook.com are:
- Server: smtp-mail.outlook.com
- Port: 25 (or 587 if 25 is blocked)
- Authentication: Yes
- Encrypted Connection: TLS
- User name: Your email address
- Password: Your password
Configured as described above, you should be able to send email from your desktop email program via Outlook.com.
POP3
Your email program uses the POP3 protocol to download email from your email service provider’s server.
The POP3 configuration parameters for Outlook.com are:
- Server: pop-mail.outlook.com
- Port: 995
- Encrypted Connection: SSL
- User name: Your email address
- Password: Your password
Note that you need to enable POP3 access in Outlook.com.
Click the gear icon in the upper right and then click More mail settings. Under Managing your account, click Connect devices and apps with POP:
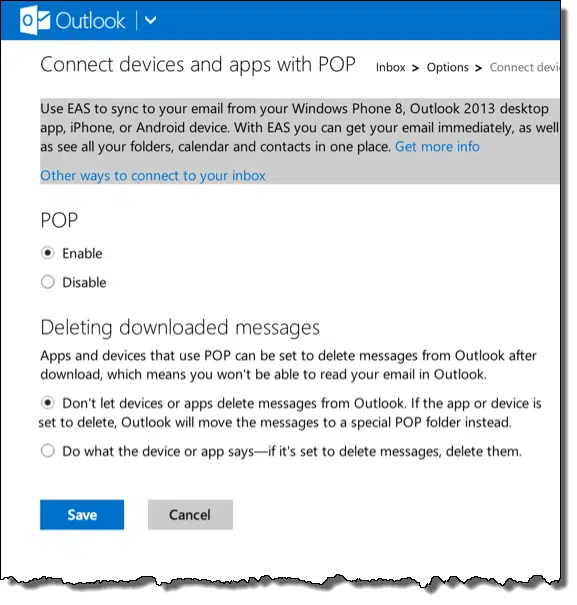
Under POP, select Enable, and then click Save.
You’ll note that you also have the option to force delete requests to be ignored. This is more-or-less the equivalent of the “Leave messages on server” option that many desktop email programs have. If you choose the “Don’t let devices or apps delete messages…” option, then they’ll remain accessible via the Outlook.com web interface until you delete them there.
IMAP
Your email program uses the IMAP protocol to copy or mirror email stored on an email server to your desktop or device.
The IMAP configuration parameters for Outlook.com are:
- Server: imap-mail.outlook.com
- Port: 993
- Encrypted Connection: SSL
- User name: Your email address
- Password: Your password
IMAP is perhaps the most convenient way to access email across multiple computers and devices as it keeps them all in sync. The downside is that a more-or-less continuous internet connection is typically required for the best experience.
Other
Microsoft also includes additional access mechanisms with Outlook.com, including Exchange Active Sync (which is apparently similar in functionality to IMAP). You can see a full list here on Microsoft’s site: Set up an email app with Outlook.com.

Important Please Read
Comments complaining about how this feature doesn’t work for you will be deleted.
Hotmail is unbelievably large, and they have a long history of rolling out changes slowly so that not all users get access to new features at the same time. Follow the instructions precisely, and if it doesn’t work, wait a few days, or even a few weeks and try again.
11-Feb-2009
One question: after setting this up, does one still have to log on via the web interface to keep your account “live”? Or does accessing your mail via POP count as “logging on”? (I’d also like to see them introduce forwarding to a mail account outside of the Microsoft world, but having POP is a good start!)
18-Feb-2009
How to configure Hotmail in my Windows mail (which is a built-in mail program in my Vista ultimate.) Everytime I go for creating a new account it says …..
“Windows Mail no longer supports the HTTP servers used by Hotmail and other web-based e-mail providers. Click the Back button to set up a different e-mail account, or see other options for accessing your web-based e-mail.”
Help is appreciated.
20-Feb-2009
Thankx Leo for answering my question.
But that’s not the problem here for me, i just searched internet for a work around on this.
So here is the solution for “Windows Mail no longer supports the HTTP servers used by Hotmail….” in Vista Windows Mail.
When creating new email account just type a fake email address like “username@xxxx.com”, then after entering all the settings needed for a POP3 account mentioned in this post, don’t connect to internet and change your fake Account email from Tools>Accounts>… to REAL email address like “username@hotmail.com” .
This should work.
And for accessing Hotmail Pop3 another than supporting countries,It’s working for me – at India, just follow this HACK at http://www.mydigitallife.info/2009/01/22/hack-to-enable-hotmail-pop3-and-smtp-support-instantly-for-all-countries/
I already mentioned a couple of times that one used to be able to access hotmail directly from outlook express or outlook but then some years ago Microsoft turned it into a paying service.
Those who already had an email address from before that time could keep on benefiting from this service for free (I’m still using it).
Dave, this service counts as access. Don’t know about the POP3 access.
Leo, I’m a little reluctant on using the POP3 service for several reasons:
– Dave’s remark
– Your response to that
– the fact that the httpmail is still working for me
– the fact that Microsoft has turned this into a paying service in the past and might do it again
– or they might decide to simply cancel the service
I must note however that I’ve been using hotmail for over nine years now and except for the one time complete removal of all my messages by hotmail (without any kind of apology…) have always been able to use it within Outlook.
Hey, thanks…but one problem….
After I typed in pop3.live.com and that other one lol.
But after clicking Finish, it should me this message:The connection to the server has failed. Account: ‘pop3.live.com’, Server: ‘pop3.live.com’, Protocol: POP3, Port: 110, Secure(SSL): No, Socket Error: 10060, Error Number: 0x800CCC0E
(Im using WIndows Live….does that make a difference?)
I dont really understand this pop3 and stuff like that so…..yea, Im stumped lol
07-Jun-2009
This the error report i recieve after following your instructions to a Tee. I`m almost ready to give up.
The connection to the server has failed. Account: ‘POP3.live.com’, Server: ‘SMPT.live.com’, Protocol: SMTP, Port: 25, Secure(SSL): Yes, Socket Error: 10060, Error Number: 0x800CCC0E
It’s clear from the error message that you’ve mistyped the name of the sending server in your account configuration. It’s smtp.live.com – you have smpt (the p and t are reversed).
– Leo16-Jul-2009
Thanks. Extremely helpful. Can I please ask one question. Having sent a message from Outlook Express, the sent folder in hotmail accessed via the web does not show a copy of that message (i.e. not sync’d). Is that expected or have i likely done something wrong? Many thanks
14-Aug-2009
If you find that incoming mail is fine but outgoing doesn’t work, it’s worth remembering that some ISPs like to block all SMTP usage except via their own servers – O2 Broadband and TalkTalk are two examples in the UK. To keep it simple you have to set up the POP3 settings as in the article but use your ISP’s own SMTP server. The set-up for this is different depending on your email software but if you already have an account set up using the ISP’s own email domain it should be fairly straightforward to find and copy the settings – as long as you know the password!
In regards to this post:
“FIXED! (Work around) You can receive but not send email using HOTMAIL’s new POP settings.
Use the settings on this page BUT…
For outgoing mail, DO NOT USE smtp.live.com – use whatever your default server is (mine is smtp.west.cox.net). I figured this part out on my own because when I use my domain mail, this is how it is set up. (Use port 25 for outgoing messages).
And if using anti-virus e-mail scanning like NORTON, go to OPTIONS / EMAIL and UNCHECK “scan outgoing messages”. (Incoming are still scanned for your protection.)
Microsoft (LIVE) and Symantec (NORTON) need to get together to resolve this issue…
Source: http://support.microsoft.com/kb/329820/en-us“
I found that this work around finally allowed me to send mail. Ports 25 and 587 didn’t work for smtp.live.com but my original pop smtp server smtp.mts.net does with port 25. Even my ISP couldn’t figure out why it wasn’t working for me. I use Incredimail as an email program and most ISP’s don’t have any information on how to configure settings in that program. Thank you for the work around!! You gave a simple solution after hours of grief.
I cant beleive, that it is that difficult to set up an Microsoft Product (Outlook 2007) to Work with a Microsoft Email Service.
I tried for hours now to set up Outlook for MSN. After a reinstall i use Windows 7 x64 an Outlook 2007 Professional.
Therefore i used windows XP x64 and Office 2003 Professional. With 2003 it was dufficult, but after changing the pop3 server port it worked.
Now Outlook is asking mer for my password again and again.
My password is right, because i log in to msn with it.
Any Ideas?
Thank you so much for this it’s great to have the messages download automatically and works perfectly.
Just a short answer to Thomas… I had the same problem until I realised my email password was different to the MSN messenger one, maybe that’s your problem too. Good luck
Microsoft allowing non-Microsoft programs to access Hotmail? I wonder what the catch is?
I wonder why then are they are then trying (and failing) to restrict the web version of Hotmail to only IE/Firefox?
Anyway, for Evolution in GNU/Linux, the following settings worked for me:
(receiving email tab)
Server type: POP
Server: pop3.live.com
Username: xxx@hotmail.com
Use secure connection: SSL
Authentication type: Password
(sending email tab)
Server type: SMTP
Server: smtp.live.com
Server requires authentication: YES
Use secure connection: SSL encryption
Authentical type: Login
Username: xxx@hotmail.com
I am not able to configure windows hot mail account in windows live mail
16-Oct-2010
Thanks for the help. I have used port 25 for years, but recently I had to switch to 587 because I was unable to send e-mail through OE. Was about ready to give up, until I read this!
I tried both 587 and 25. No luck. I was able to receive but not send. Now I can’t do either. I have 995 as the receiving and I checked the authentication boxes. Any clue?
hi, I did what you have instructed ealier but still no luck I get this error
Subject ‘Fw: Welcome to Windows Mail’, Account: ‘pop.gmail.com’, Server: ‘smtp.gmail.com’, Protocol: SMTP, Port: 465, Secure(SSL): No, Error Number: 0x800CCC19
what should i do? I read upon on that error and it says some thing about registry needs to be repaired but i restored my computer few days ago to the original setting…
Can you please help me to set it up please.
thanks
19-Dec-2010
I have windows mail. I have used the settings as described above. I have an error message stating
“host smtp not found” what do I change to get smtp found?
07-Mar-2011
@Joe: Windows Mail is an email program similar to Outlook Express, described in the article. You haven’t specified which email provider you are using. You’ll have to look up the SMTP settings on your email provider’s web site and configure Windows Mail accordingly.
Your short version worked 😉
i need this email settings for my android fone 🙂
Receiving: pop3.live.com, port 995, SSL
Sending: smtp.live.com, port 587 (or 25), TLS (or SSL)
thanks mate
Thank you, thank you!! No other website I found mentioned changing the encryption from SSL to TLS for port 587. Thank you! It works!
All very nice for most POP3 clients…. but Foxmail appears to be the exception. No matter what combination of settings I use, Hotmail will not let me send e-mails. There’s no way to select TLS in Foxmail, and its version of SSL on port 587 or 25 doesn’t work. Very annoying.
i Can’t send any email.. this error showing..
The connection to the server has failed. Account: ‘Hotmail’, Server: ‘smtp.live.com’, Protocol: SMTP, Port: 25, Secure(SSL): Yes, Socket Error: 10060, Error Number: 0x800CCC0E
04-Feb-2012
An unknown error has occurred. Subject ‘test’, Account: ‘Hotmail’, Server: ‘smtp.live.com’, Protocol: SMTP, Server Response: ‘550 5.3.4 Requested action not taken; We noticed some unusual activity in your Hotmail account. To help protect you, we’ve temporarily blocked your account.’, Port: 587, Secure(SSL): Yes, Server Error: 550, Error Number: 0x800CCC69
@Mr. Pervas
Here’s an article which discusses that issue:
Why am I repeatedly locked out of my Hotmail account, and what can I do about it?
I am using my android phone for checking 3 different pop3 and smtp email accounts, all working fine. For hotmail, however, despite following all the steps written here, I have not been able to send mail. The error message I get is “Setup could not finish. Unable to open connection to server”.
The incoming works perfect. I’ve tried to use both port 25 and 587 for outgoing but I still can’t send email message. I have even alternated between all security types, SSL, SSL (Accept all certificates), TLS, TLS (Accept all certificates) and even the None. No good though. Please help. Thank you!
How do you disable the IMAP “IDLE” function in Outlook 2010? In other words how to you stop the “PUSH” of emails so they do not get sent from the server to my application as soon as they are ready but instead will stay on the server until I request to receive emails. Other email applications such as Thunderbird have an option to disable (turn off) “IDLE”. Even the email notifier POP Peeper has a toggle function to check on or off for “IDLE”. One would think Outlook 2010 would provide this option to the user as well.
If you’re curious why I want to do this, it is because I want the IMAP synchronization advantages and do use “IDLE” in POP Peeper but because Outlook has issues with the desktop “Alert” for new mail (it has never worked with IMAP accounts from Outlook 2003-2010 as far as I know). The Alert will only work if you’ve got Outlook open and you’ve opened the inbox for the account where the email arrives. I believe this is because while other applications have apparently solved the problem Microsoft has not been able to resolve the issue of email getting “Pushed” through when Outlook has not been launched and/or your not on the specific receiving inbox. The email has arrived by the time Outlook get’s launched thus Outlook does not see the “Pushed” email as “new”. If I can disable the “IDLE” function for IMAP accounts then the emails would not arrive until I requested to receive them.
Could someone please help me it’s driving me nuts.I have a hotmail,(now outlook)email account and I’m trying to sync it with my android phone.I have tried doing exactly as people have suggested and adding the pop3.live.com server and ssl security, port 995 and it still won’t work.What am I doing wrong? thanks Helen
To begin with use the IMAP, not POP3 settings. Alternately, just install the Outlook.com application from the Google Play store. It’ll make it all pretty transparent.
THANK YOU LEO YOU ARE A LEGEND.up until a few days ago i was still able to use outlook express to connect to windows live/outlook.com and download to my XP computer(i know,its ancient,but i prefer it).but then suddenly i was unable to signin with outlook express with connection/password errors.searched the net for hours and hours but to no avail,with most sites including microsoft,saying it was impossible to use outlook express with outlook.com anymore.by enabling POP in outlook.com like you said,and changing incoming mail setting from ‘pop3.live.com’ to ‘pop-mail.outlook.com’ as you said,everything is back to normal.so much appreciated.gary
Hi Leo,
Thanks for a great website.
As Windows Live Mail 2012 will become unuseable from next month (according to a letter from Outlook I got recently), I tried to add my live.jp mail address to my Gmail but got the error message ‘Server denied POP3 access for the given username and password.
Server returned error: “Login to your account via a web browser to verify your account.”‘ Logged in to Outlook via web browser and did as per your instructions (to enable POP in Outlook) then back to gmail, but same error message and I AM logged in to my account via browser (logging out and re-log in doesn’t change anything)…I feel like I am going around in circles. Any suggestions please? Also since WLM 2012 is being ditched by MS, what is your recommendation for a mail client to install on my Win.7 computer to replace WLM 2012? Thanks again.
Almost sounds like you might be using a wrong password. Do you have your outlook.com password remembered in your browser? If so you may be logging in with the browser okay, but putting the wrong password in Gmail. Just a guess.
Thanks Connie,
That is what I thought too, and did a double-check: made sure my password was the correct one, even logged out from my Outlook and re-logged in manually with that password which I then entered again for the operation over at Gmail but it kept returning the above error msg. I am a bit stumped, really.
WTF Leo. I have been using outlook.com for over a year. Are U telling me I must start all over???
Never said that at all. What makes you think I did?
Don’t worry outlook.com will be here for a good while longer.
THANKS A LOT !!! Your note about enabling POP for apps and devices saved me some extra time & headache searching for why it did not work before…
Hi Leo,
I have 3 email addresses linked to my phone however after I had my laptop “cleaned” the one email address’s mail is not coming through. I deleted the account and tried to reload but it gives error “cant connect to server” pop disabled…..I am so not with the technology of today and dont know where and how to fix this…I urgently need to fix this as it is my business email not working…
Thanks
Thea
So your laptop and your phone both simply pick up email. There are very few things that could have been done to your laptop that would make it so that the phone suddenly can’t get email The only thing I can think of is that the person who “cleaned” the laptop used it to change the password on one of your email accounts.
In order to sort this out you need to work through where your email comes from. If it comes from one of the free online services (Gmail, Outlook.com, Yahoo, etc) then you can log in online and make sure you have your password and POP3 information correct. If it comes from a server with your own website, or from your ISP then you will check the email settings through those providers.
there may be some tussel b/w ms and mozilla thunderbird in the background,thats why outlook gives errors with thunderbird, for example the following smtp error
https://drive.google.com/open?id=1rfeq9i7bNrUm6SwQfCTleW9ZQIVW-Gu4
how to fix this error.
thanks.
I use Thubderbird with my Hotmail (outlook.com) account all the time and have never had that problem. It might have something to do with the SMTP settings on Thunderbird or a problem on Microsoft’s end.